Insights

ANNs have had their day in the sun, and have paved the way for the next generation of computing. In the Data Scientist’s ever growing thirst for the next big thing, quantum computing seems to be a sip of the cool quencher. The quintessential marriage between deep learning and quantum computing has been the subject for intense research and debate for a while now, and with research works like the famed “Classification with Quantum Neural Networks on Near Term Processors” published by Google Labs, quantum computing may finally be implemented in Neural Network models paving the way for faster, more efficient and exponentially accurate Artificial Intelligence, using concepts like polylogarthmic number of computational steps, in this case, expressed as (O(Logk n), k≥1). While quantum computing is far from a new concept, most data scientists, especially those focused on quantum research and the conjoining of quantum mechanics to Artificial Neural Network models agree that very few effective and accurate neural models out there are efficient to handle ML in a quantum mechanics paradigm.

Quantum Neuron training is not very different from the perceptron, and the aim is to draw quantum states that are in a uniform superposition over all vectors in a training set. To look a little closer into QNNs, it’s best to start with ANNs and the concept of the perceptron, the primary algorithm in supervised learning and K-means clustering, it’s unsupervised learning counterpart in the case of QNNs, the quantum neuron model can be expressed as:

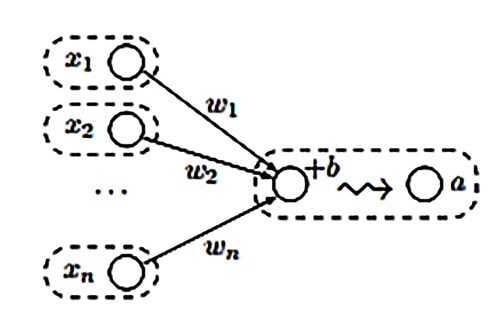
In the diagrammatical representation, x are the specific weight inputs, with bias denoted as b, form θ – which are weighted by w1, w2….

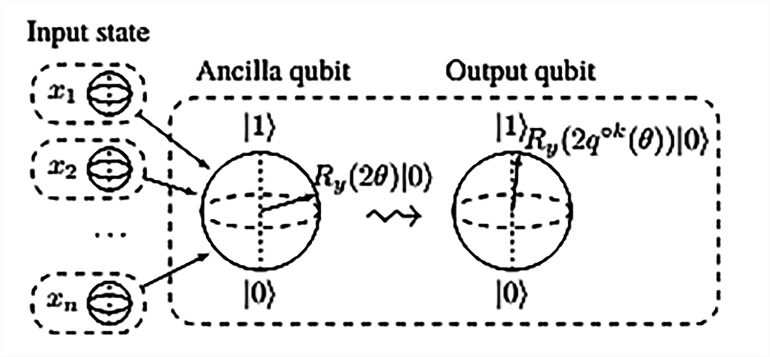
In this case, unlike the classical perceptron, the Quantum neuron produces the output (output qubit through the processing of the input qubit via the Ancilla qubit, in this case) after the Repeat Until Success technique, and corresponds to linear and non-linear activation functions, while q is a variable function with varying degrees of exponents. The neuron is continuously and internally updated as per the activation functions, respectively as denoted by the crooked arrow symbol. The input state, in most cases, are some other quantum neurons or similar components.

The Universal Quantum Perceptron as Efficient Unitary Approximator paper also posits a quantum perceptron as a non-linear excitation qubit in response to an input field as below:

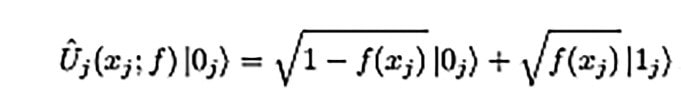
So, you think you know QNNs. If you do, the following section will help you brush up on your concepts and theories, and for the rookie, of course the neuron is critical but it is the system and structure that makes up the network. So, onwards onto the key fundamentals:

Linear Superposition – Not dissimilar to linear combination of vectors, linear superpositions are described by a wave function (ψ) that exists in what is called a Hilbert Space, which has a set of states on the basis of which the system is described by quantum states that are said to be at a superposition to those of the basis states.

Coherence and Decoherence – A first cousin to the concept of linear superposition, Coherence and Decoherence refer to the superposition of the system’s basis states. If the superposition is linear to its basis states, it is coherent, and conversely, the loss of the superposition due to any effect of the environment is called decoherence. The coefficients of coherence and decoherence, which are governed by the wave function, are called probability amplitudes.

Operators and Interference – In the context of a Hilbert space, Operators essentially explain the pattern of one wave function transforming into the other. They are usually expressed as matrices acting on vectors, basis which, an eigenvalue equation can be established.

Interference, on the other hand is a wave phenomenon, where each of the peaks which are in the phase of the wave magnify the probability amplitude of each other. Those out of the wave interfere negatively (eliminate each-others’ probability amplitude)

Entanglements – Think outside the classical neural network, and all other potential correlations among quantum states can be classified as entanglements. In the context of QNNs, when correlations exist between qubits that cannot be classified as classical, they’re entanglements. Because quantum states always exist as superpositions, when the same is affected, the correlation is communicated between the constituent qubits, which forms the essence of entanglement.

In the broadest sense of the term, most experts in the domain agree that quantum networks are likely to be more efficient and accurate if they are feed-forward, i.e., an ANN where the connections between the nodes do not form a cycle, sans any loop. Given the structure of the Quantum Neuron, a very simple Quantum Neural Network can be represented as below, allowing it to learn datasets comprising single or binary encoded outputs. In this case, every single layer is completely connected to the layer before it and computes a weighted sum of the qubits that have been outputted by the immediately preceding layer. This can be diagrammatically represented as below:

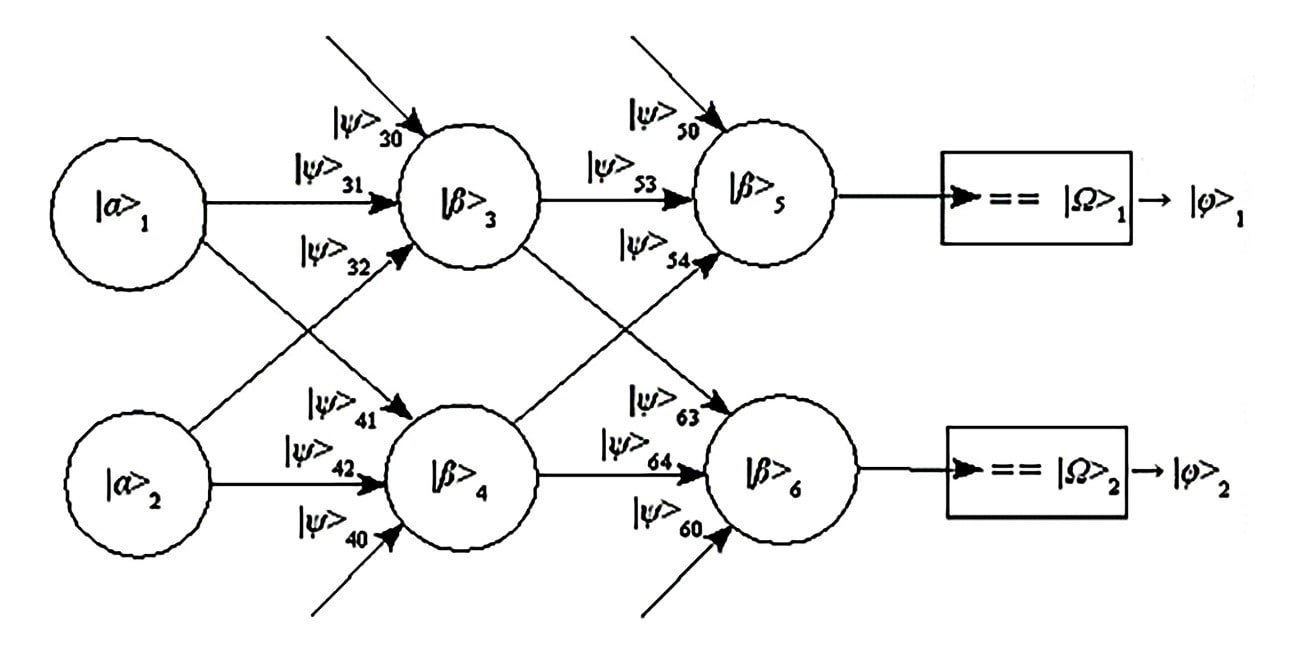
This QNN is an example of solving the XOR logic gate function. In the network, i represents input nodes, which is demarcated by a register |α>_i. The inputs (|ψ>_i1 and |ψ>_i2) are computed by the weighted sum of two hidden nodes, and is compared to the sum of a threshold weight. |β>_k represents internal calculations that occur in each node. The same process is followed by the output layer as well, which checks a weighted sum of hidden nodes against the threshold. Thereafter, each computed output is checked by the network and then compared to the targeted output, |Ω>_j, signaling a |ϕ>_j when they concur. Based on this, the network’s performance is denoted by |ρ> - computed outputs that are equal to their targeted outputs.

While it may seem that QNNs are very far from reality, given that the hardware still costs in the millions, the same could have been said of most technologies less than a decade before they went mainstream. While companies like Xanadu and Google are in the race to make quantum computing efficient and accurate, most experts agree that it is in the algorithms, the models, that the scope lies. Data Scientists out there, are you listening?