A cherished child of Adaboost and learning theory, Gradient boosting is used to analyze instances that cannot be predicted accurately. Based on an assumption that the weak learners can be modified to get better results, it uses decision trees to arrive at prediction models.
In the pure layman terms, it is the process of simplifying an otherwise complex algorithm to get the nearest accurate results.
Before we get into details, here’s a quick recap of the basic definitions:
Boosting = Building iterative models from weak learners.
Ensemble = a combination of separate models.
How Gradient Boosting Works:In gradient boosting ensembles are added in stages. In every stage, weak learners are added to compensate for the existing weak learners. The shortcomings of the combined model are identified with gradients.
Gradient boosting is used for:
- Regression
- Classification
- Ranking
The difficulty level increases from regression to classification to ranking.
Let’s try to understand this with the help of an example:
Example:
We want to predict a person’s age based on their interest in playing PUBG, visiting family or dancing. The objective of this exercise is to bring squared errors to a minimum. We have these 9 training samples with us:
| S.no | Age | Playing PUBG | Visiting family | Dancing |
|---|---|---|---|---|
| 1 | 17 | TRUE | FALSE | TRUE |
| 2 | 18 | TRUE | FALSE | FALSE |
| 3 | 19 | TRUE | FALSE | TRUE |
| 4 | 25 | TRUE | FALSE | FALSE |
| 5 | 32 | TRUE | TRUE | FALSE |
| 6 | 40 | FALSE | FALSE | TRUE |
| 7 | 43 | FALSE | TRUE | FALSE |
| 8 | 47 | FALSE | TRUE | TRUE |
| 9 | 63 | FALSE | TRUE | FALSE |
Intuition tells us:
Young people like to play PUBG.
Middle-aged like to visit their family.
And anyone could like dancing.
A rough estimate of interests set will look like this:
| Feature | True | False |
|---|---|---|
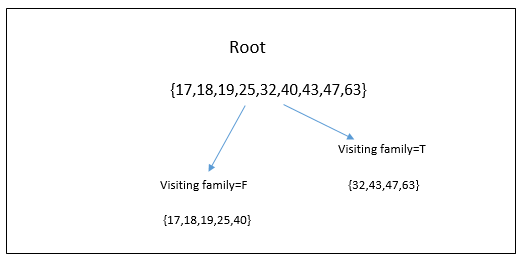
| Playing PUBG | {17,18,19,25,32} | {40,43,47,63} |
| Visiting family | {32,43,47,63} | {17,18,19,25,40} |
| Dancing | {17,19,40,47} | {18,25,32,43,63} |
And this is how its regression tree will look like:
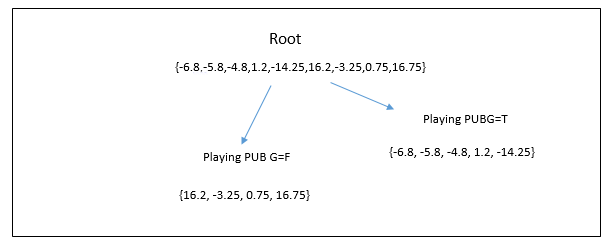
Measurement of training errors:
| Age | Tree 1 prediction | Tree 1 residual (age-prediction) |
|---|---|---|
| 17 | 23.8 | -6.8 |
| 18 | 23.8 | -5.8 |
| 19 | 23.8 | -4.8 |
| 25 | 23.8 | 1.2 |
| 32 | 46.25 | -14.25 |
| 40 | 23.8 | 16.2 |
| 43 | 46.25 | -3.25 |
| 47 | 46.25 | 0.75 |
| 63 | 46.25 | 16.75 |
We can design tree 2 based on the residuals from tree 1:
| Age | Tree 1 prediction | Tree 1 Residual(age-prediction) | Tree 2 prediction | Combined prediction(Tree 1+Tree 2) | Final residual |
|---|---|---|---|---|---|
| 17 | 23.8 | -6.8 | -6.09 | 17.71 | 0.71 |
| 18 | 23.8 | -5.8 | -6.09 | 17.71 | -0.29 |
| 19 | 23.8 | -4.8 | -6.09 | 17.71 | -1.29 |
| 25 | 23.8 | 1.2 | -6.09 | 17.71 | -7.29 |
| 32 | 46.25 | -14.25 | 7.6 | 53.85 | -21.85 |
| 40 | 23.8 | 16.2 | -6.09 | 17.71 | 22.29 |
| 43 | 46.25 | -3.25 | 7.6 | 53.85 | -10.85 |
| 47 | 46.25 | 0.75 | 7.6 | 53.85 | -6.85 |
| 63 | 46.25 | 16.75 | 7.6 | 53.85 | 9.15 |
Algorithm:
Gradient boosting can be approached in a number of ways. The simplest route can be taken with these 5 steps:
Step 1: Add additional model h to the existing model so now our equation becomes:
F(x) +H (x)
Step 2: To improve the model insert multiple points:
F(x1) + h(x1) = y1
F(x2) + h(x2) = y2
...
F(xn) + h(xn) = yn
Step 3: Reframe the equation as:
h(x1) = y1 − F(x1)
h(x2) = y2 − F(x2)
...
h(xn) = yn − F(xn)
Step 4: Fit regression tree to the data:
(x1, y1 − F(x1)), (x2, y2 − F(x2)), ..., (xn, yn − F(xn))
Step 5: Keep adding regression trees until the desired result is achieved.
The above equation can be refined to:
F0(x)=argminγ∑ni=1L(yi,γ)=argminγ∑ni=1(γ−yi)2=1n∑i=1nyi.
Gradient boosting is unbelievably efficient and its most popular algorithm is XGBoost. Gradient boosting can further be enhanced by using:
- Tree constraints
- Random sampling
- Shrinkage
- Penalized learning